Topología del Plano Complejo

Vecindades

Una $\varepsilon$ vecindad, también llamada bola abierta o disco abierto, de un número complejo $z_0$ consiste en todos los puntos $z$ que se encuentran dentro, pero no en el círculo, con centro en $z_0$ y con radio $\varepsilon>0,$ la cual se denota como

La $\varepsilon$ vecindad cerrada de $z_0$ se denota por Finalmente, una $\varepsilon$ vecindad borrada de $z_0,$ también llamada bola perforada o disco perforado, se expresa como La Figura 1 muestra la representación geométrica de los siguientes ejemplos:

Clasificación of puntos

Un punto $z_0$ se dice ser interior de un conjunto $S\subset \mathbb C$ cuando existe una vecindad de $z_0$ que contiene solo puntos de $S$; un punto se dice ser exterior de $S$ cuando existe una vecindad de este que no contiene puntos de $S.$ Si $z_0$ no es ninguno de estos puntos, se dice que es un punto frontera de $S.$ Un punto frontera es, por lo tanto, un punto en el cual todas las vecindades contienen al menos un punto en $S$ y al menos un punto que no está en $S.$ A la totalidad de todos los puntos frontera se denomina frontera de $S.$

En este texto usaremos la notación:

Considerando los ejemplos previos de vecindades, sea

De esta manera, para $S_1$ tenemos:

• $\text{Int } S_1=B_1(0)$
• $\text{Ext } S_1=\{z: |z|>1 \}$
• $\partial S_1=\{z: |z|=1 \}$

Para $S_2$ tenemos:

Finalmente, para $S_3$ tenemos:

Espacio topológico

Un conjunto $S$ es abierto si para cada $z\in S,$ existe $\varepsilon>0$ tal que $$B_{\varepsilon}(z)\subset S.$$ Esto es, $\text{Int } S= S.$ Un conjunto $S$ es cerrado si contiene todos sus puntos frontera, esto es $$\partial S\subseteq S.$$ El conjunto $\mathbb C$ es abierto y cerrado al mismo tiempo dado que no tiene puntos frontera.

El conjunto $\mathbb C,$ junto con la colección $\tau =\{S\subseteq \mathbb C: S \text{ es abierto} \}$ es un espacio topológico, y esto se expresa con la pareja $\left(\mathbb C, \tau\right).$ El espacio topológico $\left(\mathbb C, \tau\right)$ satisface lo siguiente:

1. $\emptyset$ y $\mathbb C$ son abiertos.
2. La unión arbitraria de conjuntos abiertos es también un conjunto abierto.
3. Si $S_1$ y $S_2$ son abiertos, entonces $S_1\bigcap S_2$ es abierto.

Observación: La definición técnica de espacio topológico es un poco intuitiva, particularmente para aquellos que no han estudiado topología. En esencia, esta nos dice que las propiedades geométricas de subconjuntos de $\mathbb C$ se preservarán cuando se aplican transformaciones continuas (funciones o mapeos).

La cerradura de un conjunto $S$ es el conjunto cerrado que consiste de todos los puntos en $S$ junto con su frontera. En otras palabras $$\overline{S}=S\cup \partial S.$$

En general un conjunto es conexo si no se puede expresar como la unión de dos conjuntos abiertos disjuntos. Un conjunto abierto $S$ es poligonalmente conexo si cada par de puntos $z_1$ y $z_2$ en él se pueden unir con una línea poligonal, la cual consiste de un número finito de segmentos de línea unidos de un extremo a otro, en el interior de $S.$ Un conjunto abierto $S$ es conexo si y sólo si $S$ es poligonalmente conexo.

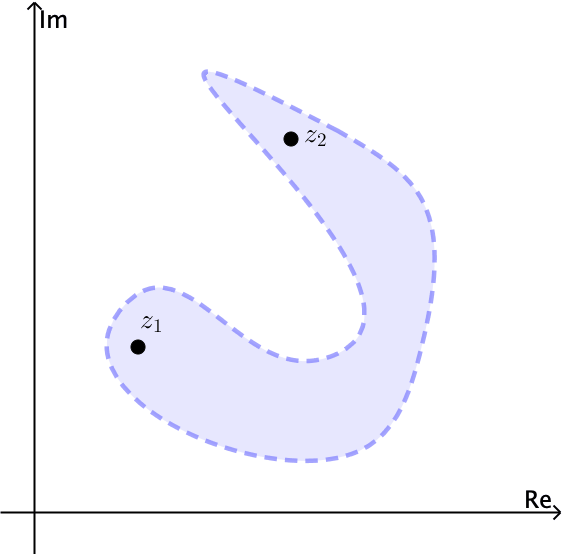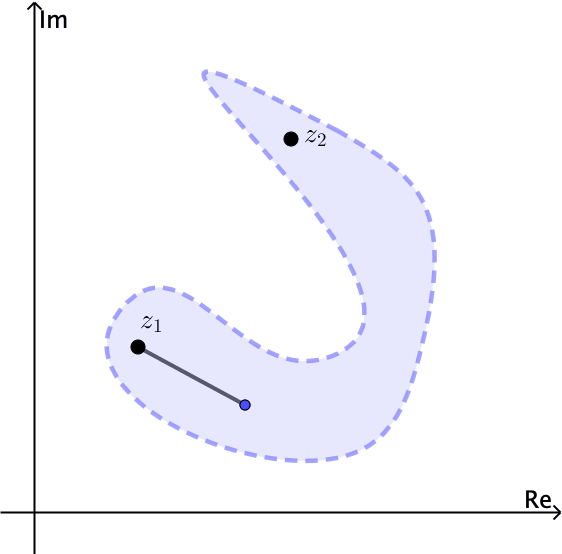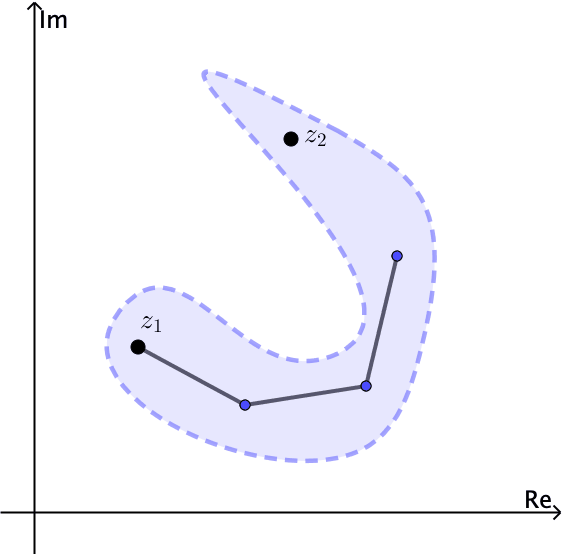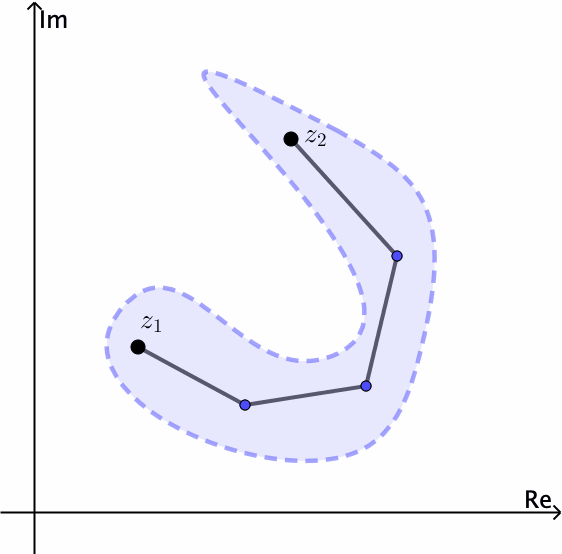
Notemos por ejemplo que el conjunto abierto $|z| \lt 1$ es conexo. El anulus $1 \lt |z| \lt 2$ es abierto y también conexo, ver Figuras 4 y 5.

Un conjunto no vació y abierto que es conexo es llamado dominio. En este contexto, cualquier vecindad es un dominio. Un dominio junto con algunos, ninguno, o todos sus puntos frontera se le conoce como una región. En otras palabras, un conjunto cuyo interior es un dominio es llamado región. Un conjunto $S$ es acotado si existe $R>0$ tal que $$S\subset B_R(0)=\{z\in \mathbb C: |z|\lt R\}.$$